In the previous article we talked about fraud proofs in general, especially how optimistic rollups (such as Arbitrum and Optimism) and how optimistic ZK proofs (such as Kailua) work, and the different tradeoffs inherent to fraud proof systems.
Fraud proofs are basically computation that can be publicly disputed before the computation goes into effect (i.e., after withdrawal period). To make the computation publicly disputable, there are two key requirements: (1) efficient on-chain challenge, in that the computation can be disputed on-chain, and (2) data availability, in that the public can obtain enough information to dispute the computation.
Fraud proofs have many tradeoffs. One can slice the computation into smaller or larger chunks, and one can have more or fewer rounds in the protocol. Fraud proofs also allow modifications. For example, user experience of fraud proofs has been impacted due to withdrawal periods. Satellite solutions such as fast confirmations can remedy the user experience by allowing third parties to facilitate verified withdrawals, often for smaller amounts, to be available instantly.
Although we often separate optimistic rollup and ZK rollup, aka fraud proofs vs validity proofs, they are two techniques that can be combined together, and this is important for our topic today—verifying fraud proofs on Bitcoin. Let us start with BitVM.
BitVM
BitVM is an innovative design proposed by Robin Linus back in December 2023. The first version of BitVM solely used fraud proofs, no ZK proofs at all, to enable programmability in Bitcoin. At a high level, the program is converted into a boolean circuit where signals take in the form of 1 and 0. The circuit consists of boolean gates that take two input wires and make one output wire. For example, the NAND gate outputs 0 if both input wires are 1, and outputs 1 otherwise. There can be many different boolean gates. The input wires are often output wires of another gate. Any program can be formatted into a boolean circuit.
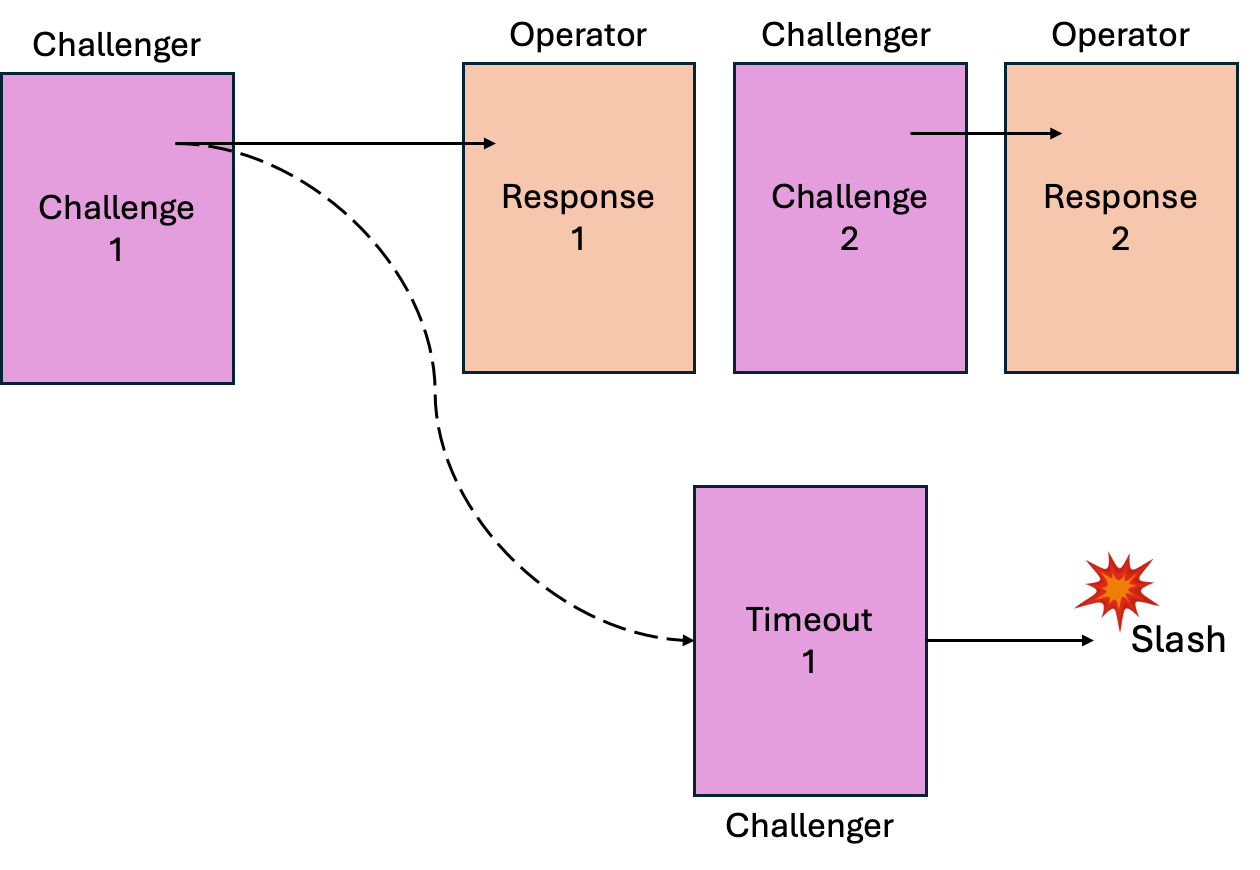
In BitVM, if the program execution is incorrect, the challenger can find at least one output wire that is incorrect. The challenger can ask the operator to reveal the two input wires for this output wire. If the output wire is incorrect, then at least one of the two input wires must be incorrect, and the challenger can continue doing so until the operator eventually (1) fails to respond according to the protocol or (2) reveals the same input wire on both 0 and 1 (being used in one gate as 0 and used in another gate as 1), which would be a contradiction.
When either of those happen, BitVM can slash the operator, and that is where the security comes from. When the operator violates the protocol, the operator will lose the “security deposit”.
If the operator fails to respond according to the protocol within a certain time window (similar to a withdrawal period), the challenger can slash the operator so that the operator loses the security deposit.
If the operator reveals the same input wire on both 0 and 1, the challenger can similarly slash the operator.
The innovation of BitVM is how to implement these two slashing conditions in Bitcoin script.
The first slashing condition is done through pre-signed transactions (generated and agreed by both the operator and the challenger) and Bitcoin native lock-time mechanism. Pre-signed transactions force the operator to follow a chain of challenge-response, in which the only thing that an operator can do at a time is to “respond” correctly to a challenge. If the operator did not respond in time, the pre-signed transactions offer an “unhappy” path that slashes the operator, which would be executable by the challenger if the operator has “timeout” from making a response.
The second slashing condition is done by having the challenger show two conflicting digital signatures of the input wires. In the BitVM protocol, when the operator reveals a certain input wire, the operator is also asked to generate a digital signature of the wire identifier and the value on that wire. If the operator misbehaves, the challenger can see two signatures, signing on the same wire identifier, but with different values. By showing these two signatures, the challenger can slash the operator.
Note that slashing alone is not sufficient for fraud proofs. As we mentioned in the Part I article, there is a subtle difference between fraud proofs and slashing:
“Fraud proofs do not rely on slashing. If the computation is wrong, there is always a way to challenge and invalidate the computation, so that the incorrect state can never be materialized on the L1 chain.”
“Slashing protocols do rely on slashing. If all the nodes are not afraid of being slashed (for example, someone bribes them to misbehave and will compensate for being slashed), even if the computation is wrong, it still can be accepted.”
This would be a problem in the first version of BitVM in that it can only achieve slashing, but it wouldn’t be a fraud proof protocol. If the operator is managing billions of dollars but only has a security deposit of a few millions, the operator is almost “incentivized” to misbehave. Making the security deposit very high is possible, but it leads to a cost usually proportional to the amount of the deposit, as the operator could have used the money in lending protocols (in CEX and DEX) to earn passive income.
This limitation is sort of inherent to the programmability of Bitcoin script (without OP_CAT). So, in August 2024, a new version of BitVM was published, called BitVM2, which focuses on a special use case where slashing happens to be sufficient for fraud proofs.
BitVM2 as a lock-and-mint bridge
Unlike the first version of BitVM which focuses on general computation, BitVM2 focuses on a specific use case—lock-and-mint cross-chain bridge. It might sound very limited that BitVM2 only supports a specific type of cross-chain bridge, but this is exactly the missing fundamental part for bridging Bitcoin to other chains in a trust-minimized manner.
Today, we do have some cross-chain solutions that bridge BTC to Ethereum and other chains, including wBTC (wrapped BTC) and cbBTC (Coinbase BTC), but they are mostly custodian based. For example, in wBTC, to mint BTC on another chain, one needs to send Bitcoin BTC to a multisig wallet, which is held by institutions in the WBTC DAO. And cbBTC is a centralized solution backed by Coinbase. There are benefits of centralized approaches in that they are flexible and sometimes with a lower cost, usually with good user experience, but it would not be a trust-minimized solution.
The lack of trust minimization is usually the cause of depegging for stablecoins because during a sudden sell-off, people may not be very confident that the custodians are solvent. There are numerous examples of depegging, and while most are temporary as in the case of Tether and Circle, some stablecoins vanished away after depgging, such as TerraUSD. Kraken has an article talking about the history of stablecoin depegging.
Depegging with BTC hasn’t really happened much, but wBTC also once had a minor depegging, which was temporary, when Alameda and FTX fell apart in December 2022.
A more recent and related example for BTC is THORChain. It is not a stablecoin or a wrapped BTC, but a lending protocol in which users can use BTC as collateral and lend other assets such as RUNE. The lending protocol itself, however, has the issue of “Death Spiral Dynamics”, in that when people lose confidence in RUNE and want to redeem BTC back, RUNE price will continue to drop. Although wrapped BTC is not a lending protocol, we can learn a lesson from THORChain, in that it is important that the protocol is designed in such a way that under “any market conditions”, one can redeem BTC back 1:1.
This leads to the core motivation of BitVM2—building a lock-and-mint bridge. Say that we have a bridge between Bitcoin and Ethereum.
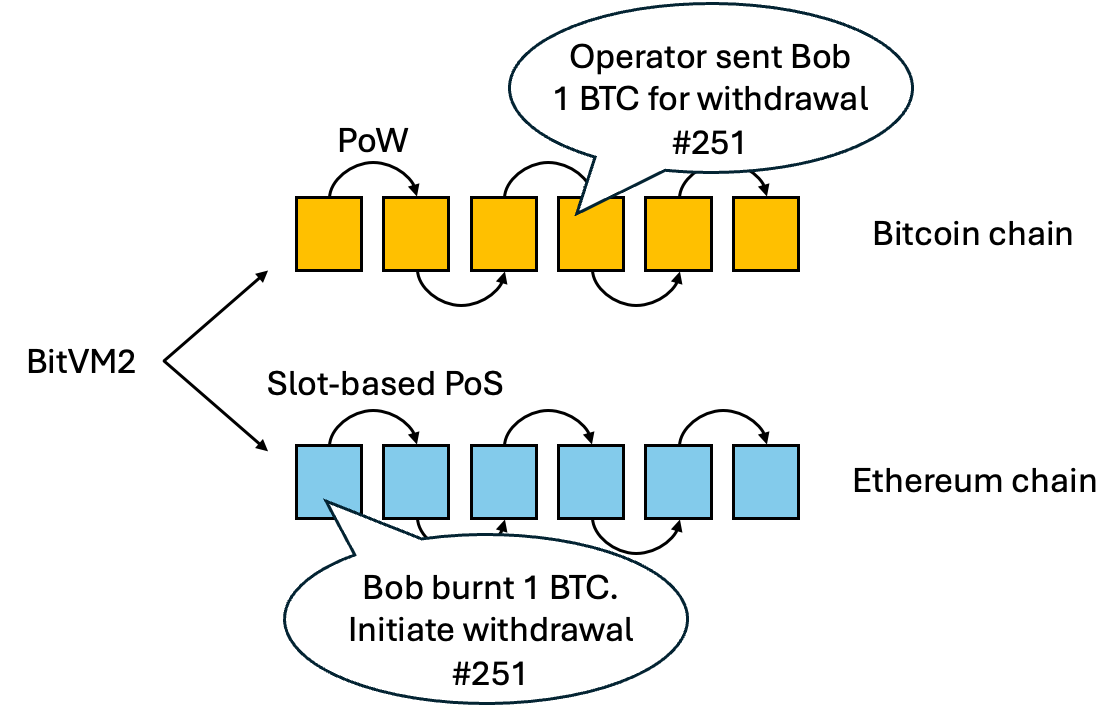
To mint a new wrapped BTC in Ethereum, Alice locks 1 BTC in Bitcoin into a BitVM2 program. It is publicly verifiable that this BTC has been correctly deposited into a valid BitVM2 program.
To redeem the wrapped BTC in Ethereum back to a native BTC in Bitcoin, Bob sends the wrapped BTC to a smart contract in Ethereum, which would “burn” this wrapped BTC. Then, an operator finds a suitable BitVM2 program with a locked BTC. The operator sends one native BTC to Bob on the Bitcoin network and then executes the BitVM2 program with a claim that the operator has correctly sent the native BTC to a user according to the unwrapping protocol. People can challenge this claim.
If the claim is not challenged, the operator receives 1 native BTC, which equals the 1 BTC that the operator sent Bob previously. If the claim is challenged and proven incorrect, the operator will not receive the 1 native BTC, as the BitVM2 program is not convinced that the operator actually sends one BTC according to the protocol.
In this use case, slashing and fraud proofs are equivalent because if the operator misbehaves, the operator simply does not receive the 1 BTC that the operator fronts to Bob previously.
An advantage of this design is that, although that BTC was originally deposited by Alice, it could be redeemed to another user, here Bob, as long as the cross-chain protocol agrees that this withdrawal is correct (per the logic defined in the BitVM2 program). This flexibility can be attained because the BitVM2 program runs a general-purpose ZKP verifier. As long as the logic, even if very complicated, can be precisely programmed into a zero-knowledge proof, BitVM2 can verify it.
BitVM2 program workflow
The detailed transaction flow in BitVM2 is complicated due to a few optimizations and security mechanisms. But the BitVM2 whitepaper also presents a simplified workflow, as follows, that should be sufficient for us to understand how it works.
When Alice deposits the 1 BTC on the Bitcoin network, it starts the deposit transaction as shown above. After the deposit, the protocol can mint a new wrapped BTC on the other chain, after verifying that the deposit is done correctly to a BitVM2 program (which can be done using a cross-chain messaging protocol).
The BTC can stay locked in the BitVM2 program for a very long period of time, until it needs to be redeemed. As we discussed above, a BTC locked by Alice can be redeemed to a different user, say Bob, as long as it fits the prescribed logic, and therefore the operator can pick any available locked BTC for unwrapping.
To redeem, the operator first fronts the capital by giving 1 BTC to Bob on the Bitcoin chain. The operator then generates a zero-knowledge proof, which can be verified (aka challenged) by the BitVM2 program. The initial state of which would be z_0 as shown in the figure above.
The operator triggers the "Request payout” through a transaction, including the initial state z_0 as shown in the graph. At this moment, anyone on the Bitcoin chain can see that an operator is currently requesting a payout (due to correctly redeeming 1 BTC to Bob). If this is correct, and during the entire challenge period, nobody has challenged this proof, it reaches the “Payout” transaction on the right where the one locked BTC would be given to the operator (who fronted the capital previously to Bob).
However, if the proof is incorrect, one can challenge the proof by sending a “Challenge” transaction, in which the operator needs to reveal the intermediate computation results through an “Assert” transaction. The information in the “Assert” transaction is expected to meet the data availability needs for a fraud proof to be generated. If the challenger finds something wrong, the challenger can disprove the computation. If within the challenge period, nobody has disputed the computation, the operator can continue to redeem the 1 BTC. If no “Disprove” transaction is made within the challenge window, the operator can continue the “Payout” transaction.
The core mechanism of BitVM2 is to disprove incorrect computation. The computation here, related to wrapping and unwrapping, involves two chains’ latest states, essentially running two light clients.
First, the BitVM2 program is running a Bitcoin light client. It needs to verify that the operator has correctly sent Bob 1 BTC already (and this transaction corresponds to this withdrawal, not a previous withdrawal) on the Bitcoin blockchain. For the BitVM2 program to do so, it not only needs to examine the specific transaction for the transfer to Bob, but also verify that the transaction is on the actual Bitcoin chain, not a side chain, not a fork.
Second, the BitVM2 program also needs to run a light client that verifies the other chain where wrapped BTC are minted, for example, Ethereum. The light client will need to verify the lock-and-mint smart contract on the Ethereum blockchain has burnt a wrapped BTC, and this very BTC has been assigned to Bob.
There are solutions on how to implement the light client, with different trust assumptions and different difficulties of implementations. But usually, the computation necessary to run the two light clients is enormous in that the “Assert” transaction would be too large or the “Disprove” transaction becomes too complicated. To address this limitation, BitVM2 uses zero-knowledge proofs, in that the entire computation is wrapped into a zero-knowledge proof, and instead of doing the actual computation, the BitVM2 program merely verifies the zero-knowledge proof.
Here, we are not using the privacy property of zero-knowledge proofs, but scalability, in that the cost to verify the proof can be significantly smaller than doing the computation.
BitVM2 as a case study
Remember that in Part 1 article, we presented an information card for BitVM.
-------------
BitVM (as in BitVM 2 bridge)
-------------
Committed computation:
- verification of a ZK proof that proves the execution of the transactions
Methods to prove guilty:
- refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------We can see that the BitVM2 bridge falls under the standard fraud proof paradigm, and the only difference from optimistic rollups like Arbitrum and Optimism is that the computation being verified is first wrapped into a zero-knowledge proof, and the on-chain computation is to verify this zero-knowledge proof. The reason for using zero-knowledge proofs is to reduce the on-chain computation overhead to make the challenge-response protocol on the Bitcoin blockchain affordable.
The same technique can also apply to Arbitrum or Optimism to reduce the rounds of interaction in the challenge period, as RISC Zero’s Kailua suggests.
Limitations of BitVM2 bridge
We now talk about some limitations of the BitVM2 bridge, as already listed in the BitVM2 bridge paper. Many other issues that people used to have around BitVM2 are mostly solvable with some engineering efforts, but these are open problems of BitVM2 that are somewhat inherent due to the restrictions of Bitcoin script.
Requires a committee to presign transactions. Since Bitcoin script doesn’t have opcodes that enable covenants, additional trust assumptions are needed for the BitVM2 bridge to work, in that one needs a committee of members to generate and presign the transactions that the operator will use. These transactions will be chained together, and the operator must follow the order to invoke these transactions. Before Alice makes a deposit of 1 BTC into the protocol, Alice can examine if these transactions are correctly generated and only continue to deposit if they look correct. The security relies on at least one of the members of the committee to delete the key used to sign the transactions, otherwise, if the entire committee colludes with the operator, the system becomes insecure.
Large, non-standard transactions. The BitVM2 bridge may have “Assert” and “Disprove” transactions that exceed the 400KB standard transaction size (which is like a soft limit), but below the 4MB hard limit. A non-standard transaction can still be accepted to the Bitcoin chain, but it often requires the collaboration of a miner, which is doable but could be costly.
Fixed deposit amounts. The chain of transactions that the committee generates and presigns will fix a specific deposit amount, and Alice needs to deposit exactly that amount of BTC. Later, when Bob redeems the BTC on the Bitcoin chain, it would need to redeem a whole BTC, and it cannot partially redeem some of Alice’s locked BTC. Although it is possible to provide some flexibility on the amounts by pre-generating BitVM2 programs for different amounts (e.g., 0.5 BTC, 0.25 BTC, 0.1 BTC), it is not going to be as flexible as if users can specify any amount. In addition, the deposit amount cannot be too small because there is a cost to run the BitVM2 protocol.
Operators must front BTC during peg-out. The protocol requires that the operator must front the BTC and then claim a “payout” for this BTC from the BitVM2 bridge. Because BitVM2 bridge has a challenge period, the payout to the operator will not be immediate, and the operator needs to have extra BTC to redeem more users. If there is a mass redemption, there is a possibility that the operator does not have enough liquidity in BTC to respond to all the redemption requests and has to “wait” until the payout arrives, which can take one or two weeks. In other words, a mass redemption in BTC can still be handled, but it would have to be slowed down depending on the liquidity that operators have.
Light client security. A careful design is needed for light clients to be secure, specifically because Bitcoin script does not have magic opcodes that allow a script to introspect the Bitcoin blockchain or even learn about the latest block # or the time. A more practical solution so far until new opcodes are added is to use several third-party services, which can include Chainlink CCIP and zkBridge.
In addition, we also have the assumption that at least one of the operators would be willing to participate in the protocol, and therefore usually BitVM2 bridge needs to have multiple operators working for the same BitVM2 program, so that even if one of them does not participate, other operators may. This, of course, has a censorship risk.
Decentralization can be tricky. The specific way that the challenge protocol in BitVM2 protocol works also restricts that operators need to be permissioned for each BitVM2 program, and cannot be sourced directly from the public (or from a proof-of-stake protocol). A remedy is to have a satellite protocol with security deposits that compensates a user when operators do not respond to requests, but it can only issue compensation up to the security deposits.
To put it differently, without new opcodes being added to the Bitcoin chain, Bitcoin programmability is still naturally restricted to what BitVM2 bridge can offer, as we discuss above.
OP_CAT or other covenant opcodes
There has been a lot of discussion about opcode upgrades in the Bitcoin chain. Although there have been many proposals, most of them are around “covenants”, as listed in the discussion page in Bitcoin Wiki.
Covenants are basically Bitcoin transactions in which the corresponding Bitcoin script has the ability to look at the inputs and the outputs of the transactions. Previously, the Bitcoin script did not have these capabilities. All the Bitcoin script can do is to verify signatures on the transaction or check a few spending conditions such as lock-time for the UTXO that the script originates from, and it is why the BitVM2 bridge design has to rely on a committee to generate and presign transactions in order to enforce the workflow for the operator.
To change the situation and bring more programmability to Bitcoin, people are thinking about an opcode upgrade to Bitcoin. There are eight opcodes and one additional opcode flag being discussed, including:
OP_CCV: CCV is short for “check contract verify”. It checks that the given input or output of a transaction is under a P2TR public key tweaked by a taptree. This opcode is intended to be used with OP_CAT.
OP_CAT: CAT is short for “concatenation”. It is a simple opcode that pulls two strings from the top of the stack and combines them together into one string.
OP_CTV: CTV is short for “check template verify”. Its functionality is somewhat similar to CCV, but based on a different implementation that is restricted to P2TR. It computes a hash of some information of the inputs and outputs of the transaction. This opcode is also ideally used together with OP_CAT.
OP_CSFS: CSFS is short for “check signature from stack”. It is an extension of the CSV opcode (check-signature-verify). Both CSV and CSFS allow the script to specify the signature and the public key, but CSV doesn’t allow the script to pick the message—it verifies the signature against the transaction body, while CSFS asks the script to provide the message for signatures, which enables some delegation use cases.
OP_PAIRCOMMIT: PAIRCOMMIT is an opcode that hashes two elements together, which can be used for Merkle tree verification. The same functionality can be realized by OP_CAT and OP_SHA256, but PAIRCOMMIT being a more restricted and specific version has the benefit that it doesn’t enable covenants, so it avoids potential risks and issues due to covenants.
OP_INTERNALKEY: INTERNALKEY is an opcode that reads the taproot internal key for P2TR transactions. This opcode serves a very specific purpose and is mostly for lightning networks. Its functionality can somewhat be captured by OP_CCV.
OP_VAULT: VAULT is an opcode for implementing a standard deferred withdrawal vault, which is commonly used to prevent wallet hacks. The idea is that a withdrawal from the vault will be made visible on the Bitcoin chain and deferred for a cooldown period, during which the withdrawal can be reverted. This is less related to general covenants, but it implements one of the popular use cases.
OP_TXHASH: TXHASH is a more generalized version of CCV and CTV in that a user can specify a transaction field selector and compute the hash of those fields. This can be useful especially with OP_CAT.
SIGHASH_ANYPREVOUT: ANYPREVOUT is not an opcode but a proposed feature flag for OP_CSV, which changes the behavior of signature verification to omit certain information on the transaction. It can somewhat be replaced by OP_TXHASH and OP_CSFS.
Developers active in the Bitcoin ecosystem have been sharing their opinions and somewhat “voting” for these protocols. Currently, the three opcodes—OP_CAT, OP_CTV, OP_CSFS—hava gained a lot of support from developers. But whether the opcodes will be added to the Bitcoin chain, and when, will require a process.
Our focus in this article is OP_CAT, as this single opcode can fulfill multiple functionalities that we need for verifying ZK proofs on Bitcoin—Merkle trees and recursive covenants. And among all these opcodes, OP_CAT is a more basic one that can already be used to build useful primitives.
We previously have shown how to use OP_CAT to build the ZK verifier for full-fledged validity proofs using StarkWare’s Stwo. It does not use fraud proofs, but just pure ZK proof verification, similar to ZK rollup, and unlike optimistic rollups. If we use it to verify (through recursive proof) a CairoVM, we will end up with a Bitcoin STARK verifier with the following properties.
-------------
Bitcoin STARK verifier (type I, validity-only)
-------------
Committed computation:
- execution of CairoVM
Methods to prove guilty: N/A
Methods to prove innocent:
- run the ZK proof verification
-------------The issue with a full proof verification—aka validity proofs—is the cost to verify a proof. With the recent fee rate on Bitcoin mainnet 1sat/vByte and the Bitcoin price around $100k, verifying a proof will take about $1250 each. If the proof is settled every 10 hours, one would be spending around $1.1m every year for proof verification.
Although it should be doable for larger rollups with good revenue like Base ($92m last year) and Arbitrum ($42m), it is not doable for smaller rollups and individual applications (which may likely need to verify more than one proof every 10 hours), or for rollups who want to settle more frequently such as Scroll and Polygon, such as 30 minutes (which would be about 20 times more expensive, to be concrete).
To avoid such a high cost, we must avoid a full verification of the proof, while preserving decentralization. This leads to the solution of using a mix of fraud proofs and ZK proofs.
-------------
Bitcoin STARK verifier (type II, optimistic verification of validity proof)
-------------
Committed computation:
- verification of a ZK proof that proves the execution of the transactions
Methods to prove guilty:
- refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------In this solution, the Bitcoin script that verifies the ZK proof is sliced into multiple segments, and the end state of each segment is revealed on-chain (so, one wouldn’t want too many segments, as it would lead to too many end states posted on-chain).
This almost removes all the on-chain cost, and the first transaction may just take a few dollars. We do not execute any segment of the Bitcoin script at this moment, so the on-chain cost, with nobody challenging it, is minimal and not related to the size of the Bitcoin script—we just need to publish a few hashes of intermediate states.
What if someone wants to challenge the proof? We can do it in two ways.
Case 1: Operator runs the segment. The challenger labels a specific segment of the script and asks the operator to rerun this segment to show that this segment can be successfully executed.
Case 2: Challenger runs the segment. The challenger executes the segment and shows that it cannot be successfully executed.
To avoid a malicious challenger who wants to challenge a valid proof and just wants to mess up with the operator, we can ask the challenger to bear the cost of the execution of that segment.
In Case 1, we have the challenger make a deposit when labelling the segment, and the operator can earn this deposit when executing the corresponding segment. The deposit will cover the transaction cost of executing the segment (with leeway for fee spike).
In Case 2, the challenger being the one that executes the segment will be directly paying the transaction fee. Similarly, since we expect each segment to be small enough after proper slicing, this cost should be manageable.
Note that, we can even move one step further, by deferring the proof generation to the time when a challenger brings it up, using the idea of Kailua from RISC Zero.
-------------
Bitcoin STARK verifier (type III, with Kailua)
-------------
Committed computation:
- execution of the transactions
Methods to prove guilty:
- requested the corresponding ZK proof verification for a section of the computation but did not provide in time
- or, after the ZK proof verification is provided, refereed delegation of computation about this ZK proof verification for a section
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------This design allows the operator to not generate a ZK proof unless a challenger asks for it, and the operator will be given enough time to generate the proof after the challenge is initiated. Moreover, in this design, the computation itself is sliced into several segments, and each time, the challenger asks for a specific segment for the ZK proof, rather than asking for a ZK proof for all the segments together.
Allowing the ZK proof to be requested on a segment-by-segment basis preserves the same security guarantees, because if the computation is incorrect, at least one of the segments is incorrect. It lowers the cost for the challenger to request a proof—since the challenger needs to pay for a deposit no less than the cost to generate the proof, the less amount of proof generation work implies that the deposit can be smaller, making the bar for challenging lower.
With these two changes, we can lower the net on-chain cost for the operator to be close to zero. This makes it suitable for applications with more frequent transactions. There are, however, a few disadvantages associated with the optimistic approach.
First, it may (or may not) take longer to achieve finality. Previously, when we perform a full verification of the proof, we need to wait for all the transactions necessary for the full verification to be settled on the Bitcoin blockchain. This already would take a lot of time, for two reasons:
The full verification consists of a number of transactions and usually will be spread out across several blocks. So, naturally, the full verification will take a few blocks to settle, around 10 blocks (which would be about 2 hours).
Operationally, since the full verification is expensive, if the fee rate is high, the operator may be inclined to wait for the fee to go down or accept a slower inclusion with a fee rate below the market price.
Using fraud proofs could make the time longer, in that we need some sort of withdrawal or challenge period to allow the challenger to examine the execution and get the challenge transaction included. Setting this challenge period is a study of its own, but in the ideal case, it is okay to assume that once the fraud proof transaction is posted on chain, within 10 minutes, a challenge can already finish the examination and submit a challenge transaction, and 1 hour can be enough for the challenge to initiate a challenge if necessary.
If the fraud proofs consist of a few rounds, the overall time for achieving finality could be longer than the full verification, but with careful design, and assuming that challengers are responsive, the finality could be achieved in a similar amount of time.
Second, it relies on challengers being online and responsive. This goal, as we discuss in the previous article, needs efforts to attain, as challengers may not have enough information/infrastructure or not have enough incentives to do so. It is especially necessary to make sure that the challengers have the software to examine the execution and submit the challenges, and that there is a sufficiently decentralized network of challengers.
Third, we are implicitly making assumptions about the lack of censorship of the Bitcoin blockchain. If, during the challenge window, all the miners decide to filter away any transaction trying to challenge the computation (for example, if miners have a financial interest in the operator’s business), then the challenge-response mechanism no longer works. Bitcoin has been known to be censorship-resistant, and there isn’t any historical event suggesting that blocking challenge transactions will happen, but we want to bring up that this is possible, especially when the challenge window is short and involves only a handful of miners.
Fourth, the program for fraud proofs is more complex. This is more like an engineering problem, but properly slicing the computation requires rewriting the Bitcoin script, and it would not be as natural as writing the full verification. Especially, remember that the previous Bitcoin script succeeds when the execution is successful, in the Case 2 of the fraud proofs, we need to revert it so that the execution is successful when the script fails (which means that the challenger detects an error). This would require a lot of work in rewriting, as our post in Bitcoin dev mailing list shows.
Conclusion
Fraud proofs have been a powerful tool in blockchain systems to provide a decentralized and low-cost way to verify off-chain computation and have seen success in optimistic rollups.
Programmability solutions for Bitcoin, including BitVM and OP_CAT-based covenants, are both using fraud proofs to either enable the programmability or lower the overhead making it affordable. This article describes how fraud proofs are used in these solutions.
Find L2IV at l2iterative.com and on Twitter @l2iterative
Author: Weikeng Chen, Research Partner, L2IV
Disclaimer: This content is provided for informational purposes only and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisors as to those matters. References to any securities or digital assets are for illustrative purposes only and do not constitute an investment recommendation or offer to provide investment advisory services.