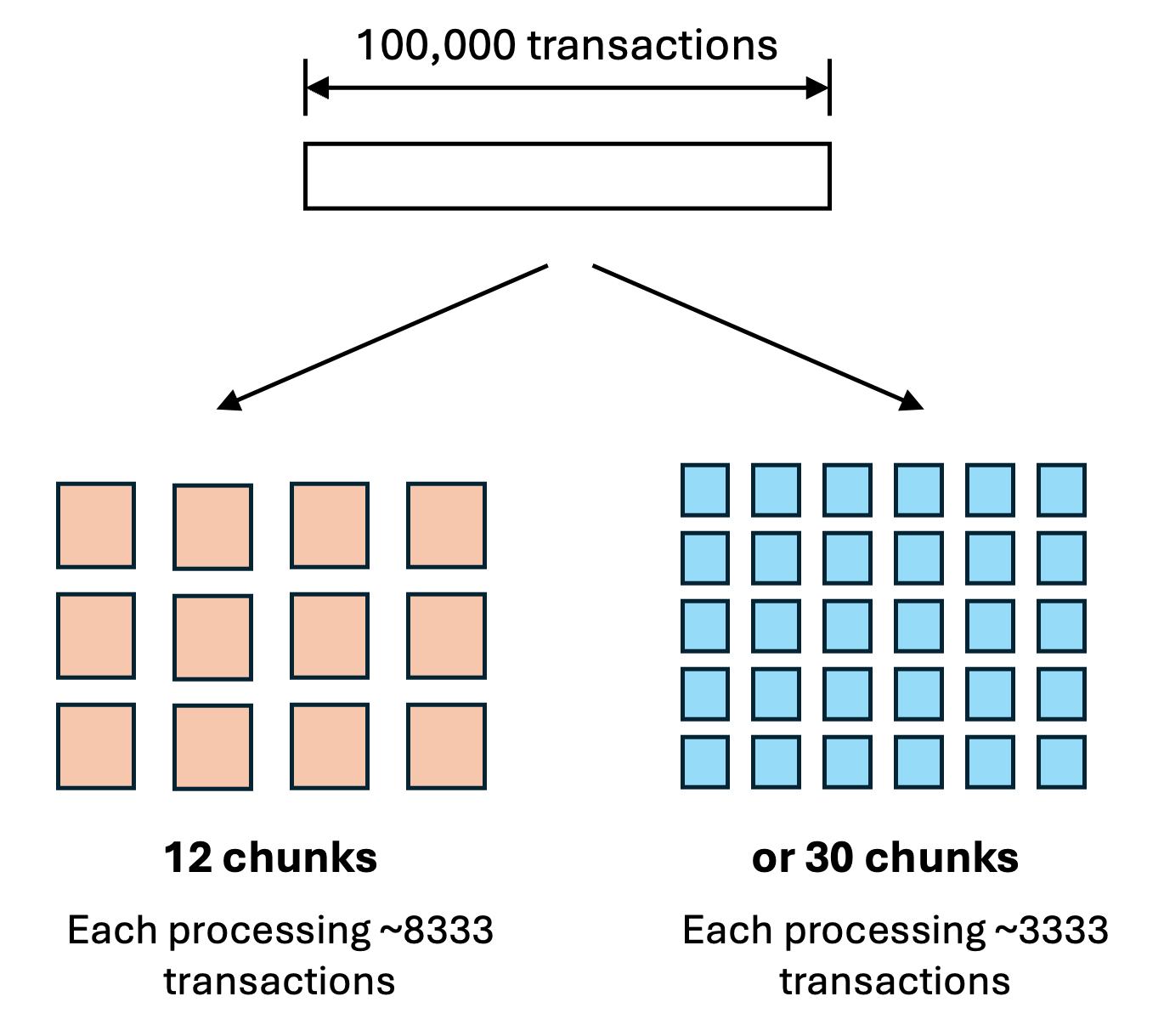In the past years, an important evolution in the blockchain ecosystem is the use of fraud proofs, as we can see in Arbitrum, Optimism, Base, and BitVM. It presents a trade-off between security and efficiency in blockchain systems.
The modern fraud proofs can be attributed to the seminal paper, “Practical Delegation of Computation using Multiple Servers”, by Ran Canetti, Ben Riva, Guy N. Rothblum, in 2011. In that paper, they built an “optimistic rollup” for x86 programs (basically any program that a computer can run), using techniques that are everywhere today for fraud proofs in EVM: bisection, Merkle hash tree, and a virtual machine.
In this article, we want to provide the background of fraud proofs. And in the upcoming Part II article, we will talk about fraud proofs in the Bitcoin ecosystem, specifically BitVM and OP_CAT-based optimistic proof verification.
Overview of fraud proofs
In fraud proofs, the computation is done off-chain, the result is being posted on-chain, and if the result is incorrect, everyone can challenge the result and invalidate the computation. Otherwise, after a period of time, often called withdrawal period, the computation is finalized on-chain.
For fraud proofs to be useful, there are two requirements:
(efficient on-chain challenge) the computation can be challenged on-chain, at a cost much smaller than running the entire computation
(data availability) sufficient information on how to reproduce the computation must be available to the public
Efficient on-chain challenge is achieved through smart contracts in EVM, the idea of which is that challenging only requires showing the smart contracts a very small part of the computation, which is cheap.
Data availability is application-specific, but, for example, in terms of an optimistic rollup, the public needs to know:
the state of the blockchain prior to the execution
the transactions
And the public expects the computation result to include a hash of all the transactions and a hash of the new state of the L2.
The public can locally execute those transactions over the prior state and see if the new state matches the result posted on-chain. If it doesn’t match, there is a fraud, and the public can challenge the rollup.
Since the prior state of the blockchain can be derived from previous transactions that appeared on the chain, the actual data availability boils down to the transactions themselves. Sometimes, data availability can be a significant part of the cost. There are different ways to reduce this cost.
Lossless compression. Arbitrum and Optimism both use Brotli, a general-purpose compression algorithm from Google, to compress the batched transaction data.
There is a reason why the compression is applied on a batch of transactions rather than each transaction individually—it improves the compression ratio. This observation was studied in a paper called MiniCrypt, which shows over a real-world dataset that batching improves the compression ratio by about 3 times. Many blockchain transactions are similar to each other, which makes batched compression even more powerful.
There still isn’t an endgame for “engineering” compression for fraud proofs, as we are still using the general-purpose compression algorithm, rather than one that specializes in Ethereum transactions. Indeed, even general-purpose compression algorithms can be made specialized by using a custom dictionary. But there is still a practicality concern, in that the complexity of the overall system would be higher with more specialized compression techniques, and whether it is worthwhile depends on the data availability cost.
Alternative data availability mechanisms. With the introduction of blobs in EIP-4844, the fees for rollups to provide Ethereum-aligned data availability have been significantly reduced. Previously, a rollup either has to store the data as regular calldata on Ethereum L1 and pays the high transaction fee or uses a third-party non-Ethereum-aligned way to store the data. Blobs introduce a cheaper option to store data on Ethereum for 18 days, which have been deemed sufficient for rollups to achieve decentralization and security.
The blob fee, however, may fluctuate. At the time of writing, to post a blob of 128KB, the cost is about $10, and this is already a 96% discount from using calldata (see [1], [2]), but still significant. In 7 months, our portfolio company Taiko paid about $3.5m worth of ETH for blobs, and our LP StarkNet paid about $700k worth of ETH for blobs. On the contrary, if they were settling the blobs on Celestia, it would be about 20x cheaper.
A project can also launch their own data availability committee, such as Arbitrum’s AnyTrust for their ecosystem chains, to further lower this cost.
Alternative data availability mechanism is an option for the rollups or applications to decide. It is okay to use it. It is okay to not use it. It is a matter of trade-off between the trust assumptions and the cost, and it can also be made secure.
For Bitcoin, the storage capacity on L1 is more limited, and therefore alternative data availability mechanism may be the only viable option. For example, a Bitcoin rollup cannot settle the data directly on the Bitcoin L1 due to the high cost and the unfavorable consequence of causing L1 congestion, defeating the purpose to use Bitcoin rollup to relieve the L1 pressure. It therefore requires an alternative data availability mechanism, ideally a decentralized one based on Bitcoin security.
Security
Now that we have an idea on how fraud proofs work, we can talk about the security of fraud proofs.
When the prover commits the execution onto the L1 blockchain, the execution has not been settled yet. For example, if account A wants to withdraw some tokens to L1, the rollup will publish this withdrawal request on L1, but the tokens have not been released to A yet.
It will need to wait for a withdrawal period, which is usually 7 days. This number, however, is sort of arbitrary and due to historical reasons (lightning network often waits for 1000 Bitcoin blocks, about 7 days). The 7-day withdrawal period may change in the near future:
Arbitrum has been implementing “fast withdrawal” on Orbit chains, which allows users to receive the withdrawals within 15 minutes. This number is set based on Ethereum finality, which is about 12.8 minutes.
Our portfolio company, RISC Zero, has released Kailua, which enables Optimism to be capable of 1-hour finality. There is a detailed study on why Kailua can provide 1-hour finality because the challenge protocol can be significantly shortened by either the challenger or the prover.
At the end of the day, the security of fraud proofs is not about how long the withdrawal period is, but it boils down to a simple question: when the rollup malfunctions, is there an honest party to run the challenge protocol and invalidate the incorrect computation? If the answer is yes, a shorter finality would work totally fine. If the answer is no, even a longer finality is not secure.
That leads to four factors of achieving fraud-proof security:
Reduce the risk of rollup malfunction: This can be done through duplication, as long as the rollup is still performant. Even for a centralized rollup, it is helpful to have different machines running the same rollup functionality, and a settlement to L1 can only happen if these machines agree on the same. It is also helpful to have different implementations of the rollup functionality (called N-version programming) to reduce the impact due to program bugs. Our LP, StarkWare, is currently working on this. Note that this is different from decentralizing the sequencers to network participants, which is more for liveness and incentive-alignment purposes, but outside nodes may malfunction just like centralized nodes, if not more.
Facilitate the honest party: The protocol needs to make it easy for the honest party to challenge the computation when something wrong happens. It is not easy to be an honest party. First of all, open-source implementation of the software for finding a discrepancy and automating the challenge protocol is needed, and its UX needs to be good enough not to discourage people from using it. Second, the cost to finish the challenge protocol should be low enough, rather than requiring the challenger to commit a large amount of capital. Third, a mechanism to prevent retaliation is needed. For example, if the honest party needs to be KYC-ed or whitelisted, they may not want to challenge at all because there might be retaliation. A solution is to use ZK, and this project “Credible Anonymous Whistleblowers” in ETH Bogotá that uses RISC Zero is a good example for making this anonymous.
Allow enough time to finish the challenge protocol: Different fraud proofs have different challenge protocols, and there are trade-offs between the amount of data that needs to be made available to the public and the number of rounds. For example, in RISC Zero’s analysis on optimistic rollup vs ZK rollup vs hybrid rollup (i.e., Kailua), for a classic optimistic rollup protocol that uses bisection, one would need D + log(N) rounds, where D is the “computation depth” and N is the number of blocks in a batch. The total number would easily go to 10 or more rounds, depending on the specific parameters. It is necessary for the withdrawal period to be long enough for both parties to engage in these rounds, with some buffer for unexpected network delays, but at the same time one needs to be mindful that a long withdrawal period hurts user experience.
Do fire drills: Normally, if the rollup operator is honest, and members of the public only challenge the execution when it is incorrect, the challenge protocol may never be used (which is often referred to as “the happy path”). But, that would result in a lack of practice: we don’t know if anyone is checking the correctness of the computation. One solution is to have regular fire drills where some “false” executions that are harmless are made by the rollup operator to test if there are still enough nodes paying attention to the system and whether they can finish the full challenge protocol.
It is important to note that fraud proofs do not equal slashing, which usually relates to EigenLayer and Babylon (both of which are our portfolio companies). It is possible for fraud proofs to have a slashing component, as an economic deterrence to the prover and the challenger for acting maliciously, but slashing is different from fraud proofs, due to a subtlety between the two.
Fraud proofs do not rely on slashing. If the computation is wrong, there is always a way to challenge and invalidate the computation, so that the incorrect state can never be materialized on the L1 chain. Slashing protocols do rely on slashing. If all the nodes are not afraid of being slashed (for example, someone bribes them to misbehave and will compensate for being slashed), even if the computation is wrong, it still can be accepted, and therefore it is important in EigenLayer or Babylon to build up the right economic incentives.
That being said, fraud proofs do not replace EigenLayer or Babylon because the problems that EigenLayer and Babylon are solving are what we call “intersubjectivity” problems, such as “is data available?” (which is why there is EigenDA) and “is 1 BTC = 1 USD?” (which needs data from centralized exchanges), the answers of which are formed through broad consensus and agreement rather than something mathematically defined or “computed”. This is also why EigenLayer and RISC Zero, two of our portfolio companies, can announce a collaboration in which ZK is used to make restaking and slashing more efficient because fraud proofs or ZK cannot solve these intersubjectivity problems that EigenLayer is solving.
In short, fraud proofs target at computation, and its security is based on computation. If there is computation to verify, fraud proofs likely will work.
Tradeoffs in fraud proofs
Now we shall take a deeper look into tradeoffs in fraud proofs.
Granularity of the computation. Consider an optimistic rollup that is committing 100,000 transactions. In fraud proofs, the computation is sliced into small chunks. Each chunk starts from some intermediate state and ends with a new state, where the new state would be used as the initial state of the next chunk.
The challenge protocol points out a chunk with at least a mistake in this chunk. It is easy to see that if the computation is incorrect, there must be at least one such chunk.
There are many ways to slice the computation, but how big should each chunk be? For example, given 100000 transactions, we can split them into 12 chunks where each chunk has about 8000 transactions, or split them into more chunks where each has about 3000 transactions. In practice, we may split more so that each chunk only deals with few transactions, to have a low on-chain challenge cost, but there is a balance.
Rounds. There is a cost in having too many chunks. To challenge the incorrect chunk, the public needs a hash of the initial state of each chunk and the new state after the computation in that chunk. There are two ways for the prover to provide these hashes, the cost of each increases with the number of chunks:
On-demand, in which the prover provides the hashes when being asked for through a bisection protocol. This takes O(logN) rounds where N is the number of chunks.
Published beforehand, in which the prover includes the hashes in the data availability layer so the public can directly use those hashes to find the incorrect chunk, without the need to confront the prover. This has the benefit that there is no round, but it requires publishing O(N) hashes.
The two methods can be used in hybrid, and each method is tunable. For example, to reduce the number of rounds, it can publish K hashes in the beginning, therefore reducing the number of rounds to O(log(N/K)). In addition, in each round, the prover does not have to strictly “bisect” the computation by offering only two hashes, but it can offer a few. Say if the prover, in each round, slices the remaining computation into S sections, then the number of rounds becomes log_S(N/K) instead of log_2(N_K). This can be significant, since it is reasonable to set S = 32 instead of 2, which would already cut the number of the rounds by 80%.
In practice, these parameters are decided by the cost of data availability on the L1 chain (as one can see, very large K or S would require a lot of data publication) and the desired number of rounds for the challenge to complete (if K=1 and S=2, there could be a lot of rounds). It is important to note that the cost differs in what we call the “happy path” and the “unhappy path”.
“Happy path” is the case when the computation is correct and nobody wants to challenge it. In this case, the only data availability cost incurred is K, the data that is published beforehand (i.e., before any rounds of challenge). There is no round.
“Unhappy path” is the case when a member of the public starts the challenge protocol. Usually, this challenger would be paying a deposit that covers the cost for the prover to respond to the challenge. This cost would include the data availability for log_S(N/K) * S hashes of the state as well. There would be S rounds, each round taking two transactions, one from the challenger, one from the prover.
It is okay to optimize for the happy path by setting K to be a small number, and the rounds in the unhappy path do not all have to use the same S. For example, it is possible that the first round in the unhappy path would divide the computation into K segments where K > S , to reduce the number of rounds.
Fast confirmation. Since the latency would impact the user experience in a fraud proof system, there have been many ad-hoc designs trying to alleviate this issue and provide some level of fast confirmation for users.
The first idea is to have some sort of “first challenge window” that is shorter than 7 days. If within this “first challenge window” nobody ever challenges the computation, then it assumes that this computation is correct and the challenge window will close early and the computation can be settled. After the “first challenge window”, even if the computation is incorrect, nobody can challenge that. But, if a member of the public senses that the computation is incorrect, it just needs to put the first challenge in within the “first challenge window”. After that, this challenger has more time to submit the subsequent challenges. This has been the core idea in RISC Zero’s Kailua on how to reduce the withdrawal period.
This idea only has a caveat, in that a malicious challenger who just wants to mess around and increase the latency can always try to challenge during the “first challenge window” so that the computation cannot be settled early. Setting a high deposit to prevent such malicious challengers is possible, but it would increase the bar for an honest challenger. It is also difficult to measure how much this deposit should be, because the loss due to delay to the users is hard to calculate.
Another idea is that, since the correct computation, even if being challenged, would eventually be settled, it is possible to “front” the capital for the users. For example, say that a user wants to withdraw just $10 USDT from L2 to L1, the L2 rollup operator can pay the user right away and, after the withdrawal period, claim the user’s $10 USDT from the L1. This significantly improves the user experience, and the rollup operator indeed does not really take risks.
This has been behind the reason why the centralized exchanges and bridges (such as Polyhedra, our portfolio company, and Orbiter Finance) allow users to deposit and withdraw money from optimistic rollup without waiting for 7 days. Specifically, they do not have to trust the rollup operator, as they can check the computation themselves from the published data. If the computation is correct, there is no way for the computation to be later invalidated.
BitVM also relies on the ability for the operator to front the capital and prove it afterwards. Of course, this would lead to an increased liquidity demand for the operator, and it could sometimes be troublesome (see [1], [2]). It would work great as long as the rollup operator fronts the capital, and the rollup operator may even be able to charge for a “fast withdrawal” fee for that. But it is not expected to work if a user wants to withdraw $100m but the rollup operator does not have that much liquidity. It also would not work if users are panicking, and there is a mass exit.
One idea for fast confirmation is to leverage ZK proof.
The extreme form is to do a full proof when needed. The idea is that if the rollup operator wants to accelerate the withdrawal period, it can do so by submitting a ZK proof that, upon being verified on-chain, immediately settles all the transactions and skips the entire withdrawal period. Basically, it is the ability to turn the optimistic rollup into a ZK rollup on-demand.
This is useful if a user wants to do a fast withdrawal of $100m and is willing to pay the rollup operator a lucrative fee to cover the cost. The operator does not need to have $100m in hand. Let us say if the operator only has $10m in liquidity, it can withdraw $10m to the user, claim the corresponding $10m from the L1 contract, withdraw another $10m to the user, claim another $10m from the L1 contract, and repeat the process until all the $100m is done. This is simply because the ZK proof, especially for this very purpose of proving one withdrawal, can be generated and verified quickly.
However, it does not have to be this extreme to have fast confirmation. Our portfolio company RISC Zero’s Kailua aims to provide fast confirmation by shortening the challenge protocol to be only a single round, in which the challenger needs to point out a section of the computation that does not sound right and request the prover to provide a validity proof. Since such a proof is expected to only take one hour to generate, the finality can be reached in about one hour (immediately when the proof is submitted).
That being said, we can summarize that modern fraud proof protocols have a lot of flexibility, and its efficiency is largely tunable. Particularly, it doesn’t have to be separate from ZK, but it is indeed somewhat orthogonal.
Fraud proofs and ZK
In the past, we treat fraud proofs and ZK to be two different families of protocols, and we used to describe optimistic rollup as “innocent until proven guilty” and ZK rollup as “guilty until proven innocent”. This did not correctly capture the fact that fraud proofs are also considered “guilty” unless, say, 7 days have passed and nobody can prove that the rollup operator misbehaves because the fund is not available during that withdrawal period.
It is helpful to think fraud proofs are like someone being detained by the police for investigation, and without a charge, the police will have to release the person after the 7-day “withdrawal period”. This does not sound like “innocent until proven guilty”, as if you trust the rollup operator, it does not have to be detained in the first place.
With this similarity, fraud proofs and ZK are not that different from each other. This leads us into the following question: if they are similar, what are some of the ways for fraud proofs and ZK to work together meaningfully?
First, Kailua can be considered as “optimistic rollup with an on-demand ZK validity proof”. The computation being committed is the execution of the transactions on the L2, and upon challenge, it can either be “proven guilty” through the existing challenge protocol or through the inability to provide a ZK proof upon request. We can summarize it as follows for Kailua.
-------------
Kailua from RISC Zero
-------------
Committed computation:
- execution of the transactions
Methods to prove guilty:
- requested the corresponding ZK proof verification for the specific section but did not have the ZK proof verified in time
- be shown by a challenger a valid ZK proof for a section that proves the execution is wrong
- or, refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------We can similarly summarize for optimistic rollup and ZK rollup.
-------------
Optimistic rollup
-------------
Committed computation:
- execution of the transactions
Methods to prove guilty:
- refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
--------------------------
ZK rollup (such as Taiko and StarkNet)
-------------
Committed computation:
- execution of the transactions
Methods to prove guilty: N/A
Methods to prove innocent:
- verification of a ZK proof for the computation
-------------Another example is BitVM, which our portfolio companies Fiamma and Nubit have been working on. BitVM differs from the examples before, in that the committed computation itself is a ZK proof verification of the execution of the transactions.
-------------
BitVM (as in BitVM 2 bridge)
-------------
Committed computation:
- verification of a ZK proof that proves the execution of the transactions
Methods to prove guilty:
- refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------Our Bitcoin STARK verifier built for StarkWare’s CairoVM, which aims to verify a ZK proof on the Bitcoin L1 assuming OP_CAT, can be run without optimistic verification, and as a validity-only system like ZK rollups.
-------------
Bitcoin STARK verifier (type I, validity-only)
-------------
Committed computation:
- execution of CairoVM
Methods to prove guilty: N/A
Methods to prove innocent:
- run the ZK proof verification
-------------But it can also add some optimistic verification, which would make it much more efficient and lightweight because the ZK proof verification is not necessary in the happy path. The optimistic verification, of course, will add some latency.
-------------
Bitcoin STARK verifier (type II, optimistic verification of validity proof)
-------------
Committed computation:
- verification of a ZK proof that proves the execution of the transactions
Methods to prove guilty:
- refereed delegation of computation
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------Note that the type II version still has a proof generation cost. Even if there is nobody from the public to challenge the proof, the operator needs to commit the verification of the ZK proof, which implies that the operator needs to generate that ZK proof even if nobody plans to challenge it. This inspires us that we can add RISC Zero’s Kailua idea to it, to create the type III Bitcoin STARK verifier.
-------------
Bitcoin STARK verifier (type III, with Kailua)
-------------
Committed computation:
- execution of the transactions
Methods to prove guilty:
- requested the corresponding ZK proof verification for a section of the computation but did not provide in time
- or, after the ZK proof verification is provided, refereed delegation of computation about this ZK proof verification for a section
Methods to prove innocent:
- not being proven guilty during the withdrawal period
-------------This version has the benefit that the ZK proof is generated only when being challenged, and the ZK proof does not have to be the full proof, but it can focus on a section of the entire computation. This is not without tradeoffs. The member of the public who wishes to monitor the computation would have to get the transactions, execute them, and check the results, while if there is already a ZK proof, they can just check the ZK proof, without the need to even download the transactions. In addition, remember that the challenge protocol would desire the challenger to pay a deposit that covers the cost for requesting the ZK proof, and this deposit would not be small and would grow with the number of transactions being executed in a section. If this deposit is too large, it becomes a barrier of entry to become a challenger.
In conclusion, we can see that fraud proofs and ZK are not separate from each other, and starting from the example of Kailua from RISC Zero, one can see that there are indeed a number of different combinations for fraud proofs and ZK to work together.
Next article
In this article, we provide the background of modern fraud proofs and show that they are a very versatile family of protocols. A number of our portfolio companies are working in related directions, including RISC Zero, Fiamma, and Nubit.
In the next article, we will focus on fraud proofs in BitVM and in OP_CAT-enabled Bitcoin STARK verifier. Stay tuned for the Part II article.
Find L2IV at l2iterative.com and on Twitter @l2iterative
Author: Weikeng Chen, Research Partner, L2IV
Disclaimer: This content is provided for informational purposes only and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisors as to those matters. References to any securities or digital assets are for illustrative purposes only and do not constitute an investment recommendation or offer to provide investment advisory services.