The Polynomial Path
A Beginner's Guide to PIOPs
The following research builds on Arantxa Zapico’s recent PROGCRYPTO presentation on Why You Should Care About Polynomials and this research paper on Interactive Oracle Proofs by Eli Ben-Sasson, Alessandro Chiesa, and Nicholas Spooner.
This article is a general overview. As the field of zero-knowledge proofs and cryptographic protocols continues to evolve at a rapid pace, it is crucial to investigate and understand emerging technologies from various perspectives.
This article represents one such exploration, aiming to demystify PIOPs and showcase their potential in reshaping the landscape of privacy-preserving computations.
Introduction
The concept of an efficient proof system, whereby a computationally limited verifier can be convinced of the correctness of an arbitrary complex computation, is fundamental to complexity theory and cryptography. At a high level, a proof system, the mathematical bedrock, allows one entity (the prover) to convince another entity (the verifier) that some statement is true, where the verifier has bounded resources and is also pivotal in ensuring the security and functionality of various digital protocols, from blockchain transactions to secure multiparty computations.
The essence of efficiency in these proof systems cannot be overstated; it directly translates to lower computational costs and broader adoption, making secure digital interactions both more accessible and sustainable, but at scale.
Historically, this quest for optimization has been advanced through the development of interactive proofs (IPs) and probabilistically checkable proofs (PCPs), each marking significant strides in our ability to conduct verifications with minimal resources.
IPs introduced back-and-forth communication between prover and verifier, evolving past static proofs.
PCPs demonstrated verifying statements probabilistically by checking small portions of proofs, pioneering "sublinear" approaches.
These laid foundations for reconciling rigorous verification with real-world efficiency constraints. But for even wider applications, a new generation of proof systems would be needed. Enter Interactive Oracle Proofs (IOPs).
Proof Systems in the Real World
In many digital systems today, one party needs to convince another that certain statements are true or computations are correct, without disclosing private underlying data. For example, a client wanting to store genetic data may need to verify that a cloud server correctly ran analytics over it without revealing the actual health data. Or a customer may need to validate that an online seller securely handled a sensitive transaction without sharing details.
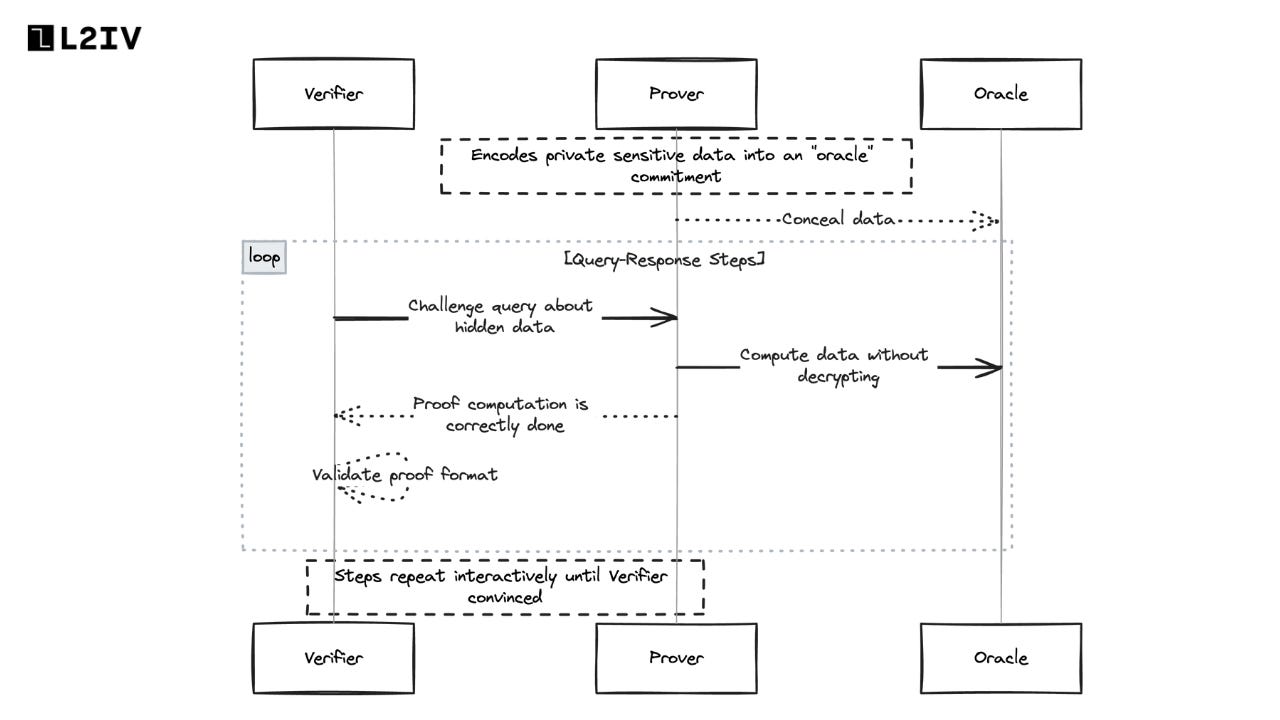
Interactive oracle proofs emerged as frameworks that allowed this convincing to happen through a back-and-forth query and response flow between the prover and verifier. The prover computationally encodes the private data into an "oracle" representation that hides the raw contents. By asking the prover to perform certain operations over this encoded data and return the results, the verifier becomes incrementally convinced without ever seeing the underlying inputs.
How IOPs Work
Prover encodes private sensitive data into an "oracle" - a cryptographic commitment that conceals raw contents
Verifier sends challenge or query about the hidden data to prover
Prover performs operations on oracle-encoded data without decrypting it
Prover sends back proof that computation was done properly
Verifier checks proof is formatted correctly
Steps 2-5 repeat in interactive back-and-forth until verifier convinced of truth
Key Features
Computation integrity verified without exposing raw data
Incrementally builds confidence through conversation
Queries and responses efficient for prover and verifier
The interactivity and encryption makes IOPs uniquely useful for web3 platforms dealing with sensitive or confidential data. By keeping data supplies and computations private while allowing validation, IOPs overcome transparency vs. privacy tradeoffs.
Interactive Oracle Proofs Meet Polynomials
The introduced interactive oracle proof paradigm offers a more practical path to verification over encrypted data. However, the techniques for actually implementing the "oracles" representing secret computations can significantly impact efficiency and flexibility.
This brings us to polynomials - algebraic structures with useful computational properties. By encoding sensitive data into polynomial coefficients, we can evaluate, transform, and reason about encrypted information without ever decrypting actual contents.
Welcome to PIOPs
Polynomial interactive oracle proofs (PIOPs) specifically utilize polynomial commitment schemes for realizing IOPs efficiently. They represent the secrets within multivariate polynomial equations, with each term consisting of variable exponents, coefficients encoding data, and modular arithmetic tying it all together.
Polynomials are a very powerful tool for constructing efficient zero-knowledge proof systems. Specifically, there is a framework called polynomial interactive oracle proofs (PIOPs) that enables a prover to convince a verifier that certain statements are true about some data set or computation, without revealing the actual underlying data or computation.
The key reason polynomials are so useful for this is they provide a way to take a very large data set and "encode" it by representing it as the coefficient vector of a polynomial. So you could have a data set with 2^20 elements, construct a polynomial with degree 2^20-1 that has each of those data elements as coefficients. This polynomial could be enormous, but has a useful feature - if you evaluate the polynomial at any given point, you get just a single numeric value out. So it takes that huge data set and "compresses" it down to one number.
This means the prover can send that evaluated polynomial value (just one number) to the verifier as a commitment that encodes all of the underlying data. Then, without ever revealing the data, the prover can prove certain statements are true about the data by manipulating the polynomial - doing operations like multiplying polynomials, evaluating them, etc. - and proving statements about the resulting polynomials using PIOPs. The verifier only sees the polynomial values, not the actual data.
This polynomial formulation enables indirect operations over concealed datasets along with zero knowledge proofs that computations were performed properly. We can multiply encodings, evaluate commitments, and prove statements about encrypted contents through algebraic rules.
So in a PIOP, the prover commits confidential data into a polynomial representation that obscures the raw underlying elements. The verifier then issues challenges for demonstrating relationships over this encoded information. As long as mathematical rules are followed, the verifier gets convinced without accessing the source secrets.
The Role of Kate Commitment Scheme (KZG) in PIOPs
Kate commitment scheme (KZG) plays a crucial role in enabling efficient and secure proof systems. KZG is a polynomial commitment scheme, which means it allows us to commit to a polynomial and later prove that the polynomial evaluates to specific values at certain points.
Imagine you have a large vector of data, like a list of transactions or a database. Instead of dealing with the entire vector directly, you can encode this data into a polynomial. Each element of the vector becomes a coefficient of the polynomial. This is where KZG comes in handy.
In KZG, the prover commits to the polynomial by using powers of a secret element in a mathematical group. This secret element is like a special key that allows the prover and verifier to work with the polynomial without revealing the actual data. The prover sends the commitment to the verifier, which is much smaller than the original vector.
Later, when the prover wants to prove something about the data, they can use the committed polynomial. For example, the prover might want to show that the polynomial evaluates to a specific value at a particular point. To do this, they create a proof using the KZG scheme, which involves some mathematical operations on the polynomial and the secret element.
The beauty of KZG is that it allows for efficient proofs and aggregation. Instead of proving each element of the vector separately, the prover can create a single proof that covers multiple elements. This makes the proof much smaller and faster to verify.
KZG is used within Polynomial IOPs (PIOPs), which are interactive proof systems based on polynomials. In a PIOP, the prover and verifier communicate using polynomials. The prover sends polynomials, and the verifier checks the polynomials by querying them at specific points. KZG enables the prover to create concise and convincing proofs within this framework.
One interesting aspect of KZG is the Lagrange basis. By encoding the data using the Lagrange basis, the prover can efficiently prove the values of individual elements in the vector. Each polynomial in the Lagrange basis is designed to evaluate to 1 at its corresponding element and 0 at all other elements. This property makes it easy to prove specific elements without revealing the entire vector.
PIOPs: Building Blocks for zkSNARKs
Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (zkSNARKs) are a powerful cryptographic tool that allows one party to prove to another that a statement is true without revealing any additional information. PIOPs play a crucial role in constructing efficient zkSNARKs by providing the underlying framework for encoding and manipulating data using polynomials.
In a zkSNARK, the prover wants to convince the verifier that they possess knowledge of a secret value that satisfies a certain computational statement, without revealing the secret itself. PIOPs enable this by allowing the prover to encode the secret value and the computational statement into polynomial representations.
The prover then uses the properties of polynomials to generate a succinct proof that the encoded secret satisfies the encoded computational statement. This proof is constructed using polynomial commitments and zero-knowledge protocols, ensuring that the verifier can verify the proof's validity without learning any information about the secret.
By leveraging the efficiency and security of PIOPs, zkSNARKs can achieve remarkable properties:
Succinctness: The proofs are very short and can be verified quickly, even for complex computations.
Non-interactivity: The proof can be generated offline and verified later without further interaction between the prover and verifier.
Zero-knowledge: The proof reveals nothing about the secret beyond the validity of the computational statement.
The combination of PIOPs and zkSNARKs opens up a wide range of possibilities for privacy-preserving applications, such as confidential transactions, anonymous credentials, and verifiable computation on encrypted data.
Let's dive into a very simplified mathematical example of how Polynomial IOPs work in the context of SNARKs. We'll use a simple arithmetic circuit to illustrate the process.
Suppose we have the following arithmetic circuit: (a + b) * (c - d) = e
We want to prove that we know the values of a, b, c, and d that satisfy this equation without revealing the actual values.
Step 1: Encode the values as polynomials First, we encode the values a, b, c, and d as coefficients of polynomials. Let's say:
a = 3, represented by the polynomial A(x) = 3
b = 1, represented by the polynomial B(x) = 1
c = 4, represented by the polynomial C(x) = 4
d = 2, represented by the polynomial D(x) = 2
Step 2: Construct the constraint polynomial We create a constraint polynomial that represents the arithmetic circuit. In this case, the constraint polynomial would be: CP(x) = (A(x) + B(x)) * (C(x) - D(x))
Substituting the values: CP(x) = (3 + 1) * (4 - 2) CP(x) = 4 * 2 CP(x) = 8
Step 3: Commit to the polynomials The prover commits to the polynomials A(x), B(x), C(x), and D(x) using a polynomial commitment scheme like KZG (Kate-Zaverucha-Goldberg). The commitments are cryptographic values that hide the actual polynomials but allow for later evaluation and verification.
Step 4: Prove the constraint polynomial evaluates to the expected value The prover needs to convince the verifier that the constraint polynomial CP(x) evaluates to the expected value (8 in this case) without revealing the actual values of a, b, c, and d.
To do this, the prover generates a PIOP proof:
The prover evaluates the polynomials A(x), B(x), C(x), and D(x) at a random point z chosen by the verifier.
The prover computes the evaluation of CP(x) at the same point z using the evaluations of A(z), B(z), C(z), and D(z).
The prover sends the evaluations A(z), B(z), C(z), D(z), and CP(z) to the verifier, along with a proof that these evaluations are consistent with the polynomial commitments.
Step 5: Verify the PIOP proof The verifier checks the PIOP proof:
The verifier verifies that the evaluations A(z), B(z), C(z), and D(z) are consistent with the polynomial commitments.
The verifier computes the expected evaluation of CP(z) using the received evaluations and checks that it matches the claimed value (8 in this case).
If the PIOP proof verifies successfully, the verifier is convinced that the prover knows the values a, b, c, and d that satisfy the arithmetic circuit, without learning the actual values.
This is a simplified example, but it illustrates the key steps involved in using PIOPs within a SNARK proof system.
In practice, the arithmetic circuits can be much more complex, and the polynomials are typically of higher degrees. The PIOP proof ensures that the prover can convince the verifier of the satisfiability of the arithmetic circuit while preserving the privacy of the input values.
Demystifying PIOPs
At the heart of PIOPs lie two key concepts:
Polynomial Encodings as Locked Boxes
A Conversational Verification Dance
Polynomial Encodings as Locked Boxes
A useful analogy is to think of polynomial encodings as special locked boxes that allow restricted operations without ever unlocking the contents.
Specifically, the prover starts by encoding sensitive raw data (e.g financial records, medical data, etc.) numerically. This long string of numbers then becomes the coefficient vector of a multivariate polynomial equation.
We can visualize this polynomial commitment scheme as taking the sensitive data and sealing it within a cryptographic box secured by mathematical locks. The box conceals all actual values, showing only the outer shell.
However, the box allows selectively applying certain keys to reshape and transform its exterior in provable ways, indirectly operating on the contents:
Special keys can stretch/compress the box by evaluating the polynomial encoding at points
Other keys can verify modular rotations orOperations that rearrange its composition
Some keys attach cryptographic proofs of valid transformations
So by asking for the right kind of manipulations and validating the keys used follow mathematical rules, we can gain confidence the concealed raw data has been handled properly without ever directly accessing it. The polynomial encodings act as data containers we can compute over while keeping contents private.
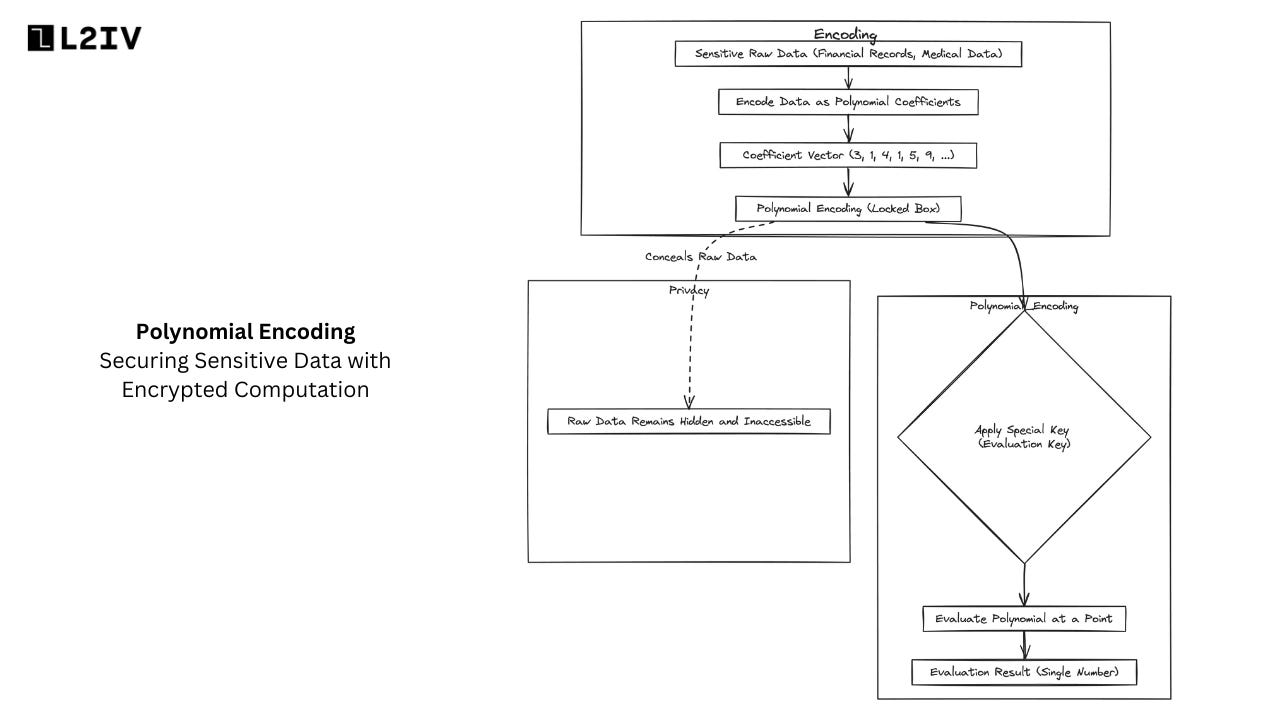
Sensitive Raw Data:
At the beginning of the process, we have some sensitive information that we want to protect. This could be things like financial records or medical data.
We don't want anyone to be able to see this data directly because it's private and confidential.
Encode Data as Polynomial Coefficients:
To keep the sensitive data safe, we need to transform it into a different form that hides the original information.
In this step, we take the raw data and convert it into a list of numbers called polynomial coefficients.
Think of it like putting the data through a special machine that scrambles it up into a secret code.
Coefficient Vector:
After encoding the data, we end up with a list of numbers known as the coefficient vector.
In the image, the coefficient vector is shown as (3, 1, 4, 1, 5, 9, ...).
Each number in this vector represents a piece of the encoded data.
Polynomial Encoding (Locked Box):
Now, we take the coefficient vector and place it inside a special "locked box" called the Polynomial Encoding.
This locked box is like a secure container that keeps the encoded data hidden from anyone who doesn't have the right keys to open it.
The box conceals the original sensitive data, so even if someone gets their hands on the box, they can't see what's inside.
Privacy:
The locked box (Polynomial Encoding) is designed to protect the privacy of the sensitive data.
As shown in the image, there's an arrow pointing from the locked box to the "Privacy" section.
This means that the raw data remains hidden and inaccessible to anyone who doesn't have permission to unlock the box.
Apply Special Key (Evaluation Key):
Now, let's say we want to perform some operations or calculations on the encoded data without revealing the actual information.
To do this, we use a special key called the Evaluation Key.
In the image, there's an arrow pointing from the locked box to the "Apply Special Key" step.
The evaluation key allows us to interact with the locked box in specific ways without actually opening it or seeing the raw data inside.
Evaluate Polynomial at a Point:
One of the things we can do with the evaluation key is evaluate the polynomial (the encoded data) at a particular point.
This means we plug in a specific value and calculate the result based on the encoded data inside the locked box.
It's like asking the locked box a question and getting an answer without ever seeing the original data.
Evaluation Result (Single Number):
When we evaluate the polynomial at a point, we get a single number as the result.
This number is the outcome of the calculation we performed on the encoded data.
We can use this result for further computations or comparisons without ever knowing the actual sensitive information hidden inside the locked box.
So, in summary, this process allows us to take sensitive data, encode it into a special form (polynomial coefficients), and lock it up in a secure box (Polynomial Encoding). We can then use a special key (Evaluation Key) to perform calculations on the encoded data without ever seeing the original information. This way, we can work with the data while still protecting its privacy.
A Conversational Verification Dance
Rather than a static proof, the verification process happens interactively through a back-and-forth "dance" between the prover and verifier.
The verifier issues a series of polynomial operation challenges tailored to confirm computations over the concealed data were done correctly. The prover manipulates the polynomial box in response to each challenge, sending back the transformed encodings plus proofs of proper execution.
As long as these responses methodically follow valid algebraic rules, the verifier becomes incrementally convinced of correct handling of the raw data. By steering this conversation and seeing keys used properly unlock intermediate proof states, assurance builds interactively.
So PIOPs bridge interactivity with polynomial cryptography to facilitate a dialogue rooted in mathematical formalisms yet flexible enough for practical applications needing to verify computations over sensitive data. The dialogue grants confidence while encryption protects underlying secrets.
In this diagram:
The verification dance begins with the "Start of Verification Dance" note, indicating the commencement of the interactive process between the Verifier and the Prover.
The verification dance proceeds with a series of interactions:
The Verifier issues the first polynomial operation challenge (Challenge 1) to the Prover, requesting a specific manipulation of the polynomial encoding of the sensitive data.
The Prover receives Challenge 1, manipulates the polynomial accordingly without revealing the underlying data, and generates Proof 1 to demonstrate the correct execution of the requested operation.
The Prover sends Proof 1 back to the Verifier.
The Verifier receives Proof 1 and verifies its correctness. If the proof is valid, the Verifier's confidence in the Prover's claims begins to build.
The Verifier issues the second polynomial operation challenge (Challenge 2) to the Prover, requesting another specific manipulation of the polynomial encoding.
The Prover receives Challenge 2, manipulates the polynomial accordingly, generates Proof 2, and sends it back to the Verifier.
The Verifier receives Proof 2 and verifies its correctness. If the proof is valid, the Verifier's confidence in the Prover's claims increases further.
The diagram also explores an optional section where the Verifier can issue further challenges to the Prover if necessary. The Prover responds with subsequent proofs, and the Verifier verifies each new proof. This process can continue until the Verifier is satisfied or until a predetermined number of challenges is reached.
After all the challenges have been issued and the corresponding proofs have been verified, the verification dance concludes with the "End of Verification Dance" note.
If all the proofs provided by the Prover are valid and the Verifier's confidence reaches a sufficient level, the Verifier sends a message to the Prover indicating that the verification has succeeded.
The Prover manipulates the polynomial encoding and provides proofs, while the Verifier checks the responses and builds confidence incrementally. The incremental building of the Verifier's confidence through multiple challenges and proofs is a key aspect of the PIOP verification process.
Comparing PIOPs
As we've seen, PIOPs offer a powerful framework for enabling efficient and secure verification of computations over encrypted data. But how do they compare to other well-known proof systems? Let's take a closer look at the key properties of Interactive Proofs (IPs), Probabilistically Checkable Proofs (PCPs), zkSNARKs, and PIOPs to understand their unique strengths and differences.

While IPs and PCPs laid the groundwork for interactive and efficient verifications, zkSNARKs and PIOPs have built upon these foundations to offer solutions that are both efficient and privacy-preserving. zkSNARKs excel in providing succinct and non-interactive zero-knowledge proofs, making them especially suitable for blockchain applications. PIOPs, on the other hand, balance the benefits of interactive proofs with the efficiency and privacy offered by polynomial commitments, making them versatile for a wide range of cryptographic applications. Each of these proof systems has its place in the cryptographic landscape, chosen based on the specific requirements of efficiency, scalability, privacy, and trust assumptions of the application at hand.
Conclusion
Throughout this article, we've explored the fascinating journey of PIOPs, starting from their foundations in Interactive Proofs and Probabilistically Checkable Proofs. We've seen how PIOPs leverage the magic of polynomial encodings to create "locked boxes" that allow us to perform computations on encrypted data without revealing the underlying secrets. The conversational verification dance between the prover and verifier showcases the elegance of PIOPs, as they incrementally build confidence in the correctness of the computations through a series of challenges and responses.
But the real excitement lies in the practical applications of PIOPs. As we've discovered, PIOPs serve as the building blocks for the groundbreaking Zero-Knowledge Succinct Non-Interactive Arguments of Knowledge (zkSNARKs). By enabling efficient and succinct zero-knowledge proofs, PIOPs open up a world of possibilities for privacy-preserving protocols, from confidential transactions and anonymous credentials to verifiable computations on encrypted data.
Of course, PIOPs are not the only players in the cryptographic proof system arena. Our comparison with Interactive Proofs, Probabilistically Checkable Proofs, and zkSNARKs highlights the unique strengths and trade-offs of each approach. While PIOPs may not always be the perfect fit for every scenario, their versatility and balance between efficiency, scalability, and privacy make them a compelling choice for a wide range of applications.
As we look ahead, the future of PIOPs and their role in shaping the landscape of privacy-enhancing technologies is truly exciting.
Find L2IV at l2iterative.com and on Twitter @l2iterative
Author: Arhat Bhagwatkar, Research Analyst, L2IV (@0xArhat)
References
Disclaimer: This content is provided for informational purposes only and should not be relied upon as legal, business, investment, or tax advice. You should consult your own advisors as to those matters. References to any securities or digital assets are for illustrative purposes only and do not constitute an investment recommendation or offer to provide investment advisory services.